5 min to read
The Colors of Music
A cool connection between music and color

The Colors of Music
Every note on a piano is defined by its frequency, for example middle A is 440 Hz. If you double the frequency, you get back the same note one octave higher. So 880 Hz is an A one octave up and 1760 is an A 2 octaves up and so on. If you keep doubling the frequency, eventually you will get to a frequency that is in the range of the frequencies of visible light. It follows that if there is a frequency in visible light that corresponds to the note A, then the color of that light also corresponds to the note A. In other words, the note A on a piano has a color associated with it. I wanted to find this color.
The first thing I needed to do was to find how many octaves up I need to go to take A 440 Hz into the visible light range. The range of visible light is about 400-800 terahertz (THz). To find the number of octaves, I wrote down an equation to find the number of doublings, $n$, it takes to get from 440 Hz to 440 THz, then worked backwards to find $n$
\[\begin{align*} 440 \times 2^n &= 440 \times 10^{12} \\ 2^n &= 10^{12} \\ n &= \log_2(10^{12}) \\ n &\approx 39.86 \end{align*}\]which is about 40 octaves. Let’s stop for a second and think about what 40 octaves looks like. A typical piano has about 88 keys, which is about 7 octaves. There are 12 keys in every octave so 40 octaves is 480 keys to the right of middle A, or about 5 pianos to the right of middle A, if we arranged them all side by side. Thats wierdly not has many as I thought it would be. It just goes to show the power of exponential growth, it only takes 40 doublings to go from 440 Hz to 440 THz!
Next I calculated the frequency of the note A 40 octaves up from 440 Hz.
\[\begin{align*} 440 Hz \times 2^{40} &= 484 THz \end{align*}\]so the frequncy of light at 484 THz is the color of the note A. We can find the wavelength of this light by using the formula $c = \lambda f$ where $c$ is the speed of light, $f$ is the frequency, and $\lambda$ is the wavelength.
\[\begin{align*} \lambda &= \frac{c}{f} \\ &= \frac{3 \times 10^8 m/s}{484 \times 10^{12} Hz} \\ &= 620 nm \end{align*}\]which corresponds to the color orange. I found the exact shade of orange by using an online wavelength to color converter, 405nm.com. Try it for yourself, the Note A is beautiful!
We can follow a similar process to find the colors of other notes. I made a quick python script to get all the wavelengths
# Import numpy
import numpy as np
# Constants
base_frequency = 440 # Frequency of note A in Hz
notes = ["A", "A#", "B", "C", "C#", "D", "D#", "E", "F", "F#", "G", "G#"]
# Calculate frequencies for each note in one octave
frequencies = [base_frequency * (2 ** (i / 12)) for i in range(12)]
# Define the conversion from frequency to light frequency (target range in THz)
def audio_to_light_frequency(audio_freq):
# Calculate how many doublings are needed to get into the THz range
doublings = np.ceil(np.log2(430e12 / audio_freq)) # Use 430 THz as the lower visible light bound
return audio_freq * (2 ** doublings)
# Calculate light frequencies and corresponding wavelengths
light_frequencies = [audio_to_light_frequency(freq) for freq in frequencies]
wavelengths = [3e8 / freq for freq in light_frequencies] # speed of light = 3e8 m/s
# Print out the results
for note, wavelength in zip(notes, wavelengths):
print(f"{note}: {wavelength:.0f} nm")
A: 620 nm
A#: 585 nm
B: 552 nm
C: 521 nm
C#: 492 nm
D: 465 nm
D#: 438 nm
E: 414 nm
F: 391 nm
F#: 369 nm
G: 696 nm
G#: 657 nm
Lastly, I used 405nm.com to make a diagram of a piano with all the colors filled in for each note. Check it out below!
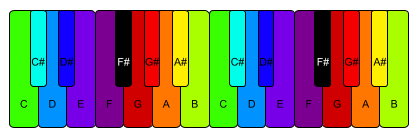
Overall, I really enjoyed working on this project and finding this cool connection between sound and sight. I’m already thinking of ways to use this mapping in future projects. I hope you enjoyed reading about it as much as I enjoyed working on it!


Comments